撰写本篇笔记的动机来源于一个真实场景中的项目需求——用户行为模式研究。我们总希望能够使用数学的语言来描述用户行为，以便能够推断用户的未来动态，用于优化系统。因此本文首先将给出上述的motivation scenario，然后介绍用于建模场景中用户行为的数学模型——Markov switching Model，以及原因。最后介绍该建模方法背后的数学工具——Markov Chain Monte Carlo。

目录

• Motivation
• Regime Switching Model & Markov Switching Model
• Markov Chain Monte Carlo (MCMC)
• 案例分析与实现
  • 开源代码调研
  • 案例分析

1. Motivation

本文的示例场景来源于“复杂移动接入网中，面向用户的体验优化与网络问题发现”。

1.1 示例场景

设有用户A，该用户在移动接入网中的行为模式可以概括为以下几点：

1. 用户A可能会随节假日/工作日的规划，接入到不同区域的网络中，而这些区域的基站由于所处位置不同，所能提供的网络性能也有差异。例如：大型居民区/城市热点区域的基站一般具有较大的容量（重服务），而郊区/或非城市主干区域则相反（重覆盖）。因此用户在上述区域内体验到的网络服务质量也有所差异。
2. 用户A在节假日或工作日内，将随机接入用户所在地附近的小区，这些小区将综合自身的服务能力、用户的业务质量要求、用户数据量，提供差异化的网络服务。用户在此过程中可感知到的网络服务水平指标通常由“速率（DLUserThrpAvgwithoutLastTTI(Mbps)）”刻画。

1.2 目标

分析用户的行为特征，目标在于借助单个用户的体验反馈，找到（频繁）影响用户网络体验的网络问题。这里，网络问题主要指“接入网”中可能存在的故障、告警、不恰当的组网策略等。

网络问题常常表征在用户级KPI的变化上，因此，分析用户级KPI上的异常链路，是帮助我们发现网络问题的必经途径。这里，异常链路指一系列时间、空间、因果上具有相关关系的指标异常。例如：用户TA异常——用户RSRP异常——MAC层指标异常——用户体验异常。在分析过程中，我们不仅关注用户的体验异常，也关注数传指标的异常，因为这两者都代表了潜在的网络问题。

下图展示了在同一小区内，用户级指标之间的机理，其中左框中为资源型指标，右框中为数传指标。实线表示指标之间的相互影响关系，虚线则表示“数传指标差时，小区将调用更多的资源来完成用户的请求”。待发现的异常链路，即为下图中的KPI节点所连接起来的一条路径。

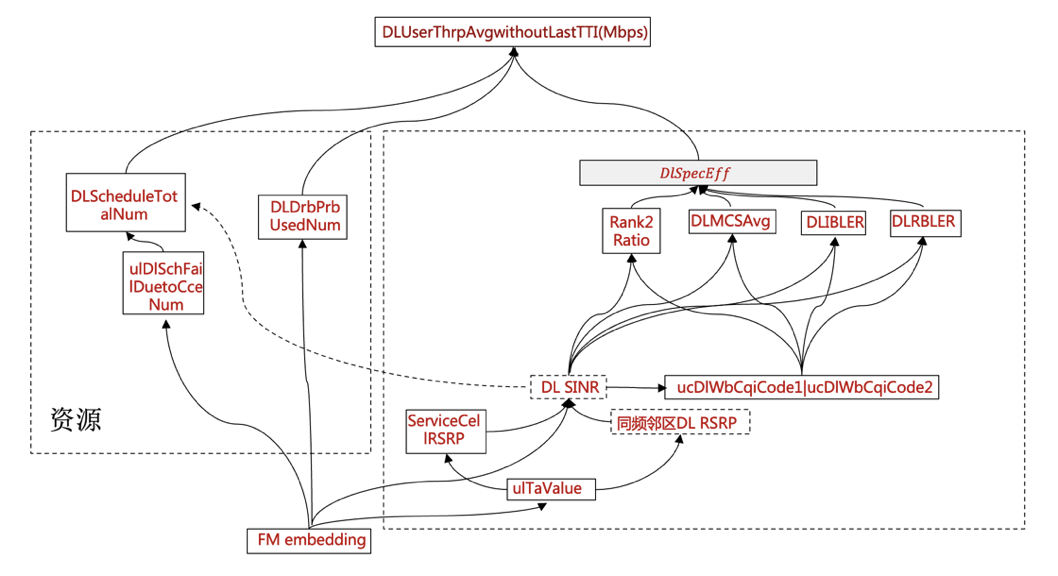
1.3 建模思路

如2.1节所述，用户的行为模式依照时间的粒度可以分为两种模式：

• 粗粒度模式：用户的行为模式可能随时在”节假日模式“与”工作模式“中切换。在每种模式在，用户的业务需求、业务类型、数据类型将有较大的差异。
• 细粒度模式：用户在每种粗粒度模式下享受到的网络服务，也将受小区状态、小区能力、昼夜的影响，有较大的差异。

因此，本研究使用马尔可夫机制转换模型（Markov regime switching model）与马尔可夫链模型（Markov Chain）来分别建模用户的粗粒度模式与细粒度模式。其中，用户的模式切换，以及所享受到的网络服务，都被视为随机变量，粗粒度模式被视为一种regime，其转换受Markov Chain所驱动。用户体验到的网络服务则被视为由参数不同的另一个Markov Chain驱动的随机变量。

2. Regime Switching Model & Markov Switching Model

2.1 Why regime switching model

机制转换模型（Regime switching model）是对非平稳、非线性时间序列建模的一类常见模型。机制难以观测、由随机过程所驱动，而每一种机制下的时间序列可以视为独立的随机过程，具有不同的参数。机制转换模型常被用于建模经济中的周期性变化影响。

使用单一的随机过程（以马尔可夫过程为例）对数据在一段时间内的变化进行描述时，其概率转移矩阵通常是固定不变的。但是这个假设对于我们在现实世界数据中遇到的许多问题并不总是有效的，原因如下：

• 实际时间序列数据在不同时间段，可能具有不同特征，例如均值和方差；
• 对于具有不同特征的时间序列数据，其在不同特征时期的模型参数（状态空间、概率转移矩阵等）可能不一样，如股市在平稳期、震荡期（宽幅震荡、窄幅震荡）；

因此，机制转换模型可以认为是最接近实际问题的理论模型，是对真实系统的一种近似，并且该理论模型的可以指导我们设计解决实际问题的方案。

2.2 Application of regime switching model in wireless access network

在无线网络中，由于各小区环境及基站配置不同，系统性能指标的变化模式也不同，具有非平稳性，且用户的移动会导致小区切换、同时小区也存在状态间切换。相比传统模型，机制转换模型通过以下设定，可以更好地刻画非平稳的时间序列，并捕捉现实世界数据的真实行为。

• 将数据描述为属于不同的、重复出现的状态（regime）
• 允许时间序列数据的特征（例如均值、方差和模型参数等）在不同状态下发生改变
• 假设在任何给定的时间段内，序列数据都可能处于任何一种状态并可能过渡到不同的状态

2.3 Markov Switching Model

由上节可以知道，regime switching model也是受随机过程驱动的，如果这个过程是一个马尔可夫链，那么我们称之为 Markov switching model。

综上，在本案例（即用户行为建模）中，我们利用两个层面的马尔可夫链来从用户级CHR数据建模用户行为：

• Markov Chain 1：驱动regime的随机变换。
• Markov Chain 2：驱动某个regime内的用户体验变化与数传指标变化。

3. Markov Chain Monte Carlo (MCMC)

MCMC由两个MC组成，即蒙特卡罗方法（Monte Carlo Simulation，简称MC）和马尔科夫链（Markov Chain ，也简称MC）。MCMC算法的目的在于“在概率空间，用随机采样的思路，估计概率后验分布”。

这里需要阐明实际问题中的几个概念：“先验分布（prior distribution）”、“可能性分布（likelihood distribution）”、“后验分布（Posterior distribution）”

• Prior：先验分布，代表了在未知真实数据的情况下，人们对于该数据分布做出的先行假设。先验分布也被称为信念（brief）分布，因为它指明了人们在未知真实数据的情况下，对数据分布的信念。
• Likelihood：似然分布，表示在已知真实数据的情况下，每个观测数据出现的可能性，它总结了已观测数据的统计意义。与之相关的maximum likelihood estimation（最大似然估计）回答了一个问题：怎样的样本值范围才最有可能让我们采样到已经观察过的数据？该问题在没有先验分布的情况下时没有意义的。
• Posterior：后验分布，这是贝叶斯分析的最终目标。旨在综合prior distribution（先验的信念）与likelihood distribution（实际的观察），来推断数据的真实分布。

在[1]中给出了一个简明的案例，用于说明三者之间的关系。

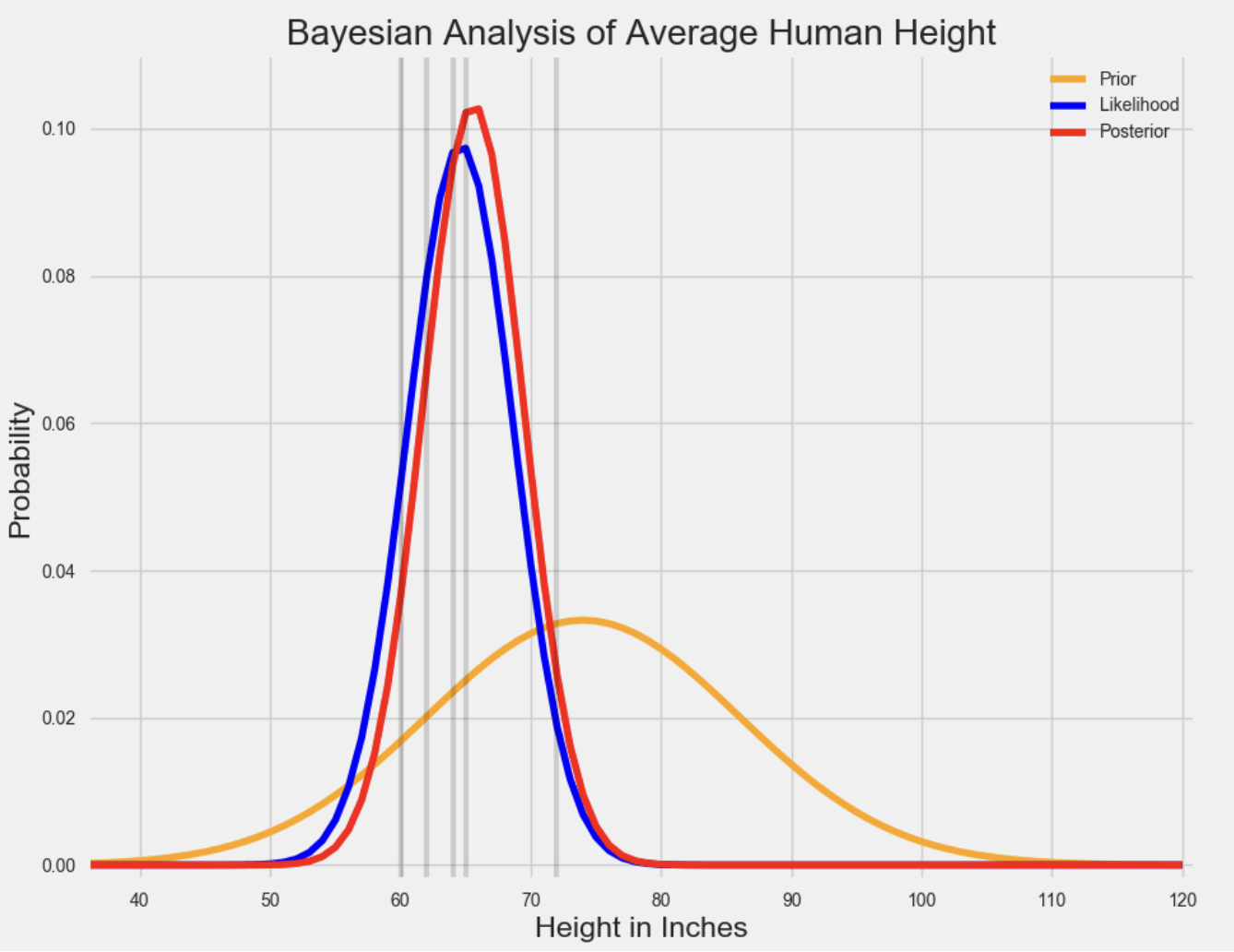
上图中，红色的曲线代表后验分布。你可以把它看作先验分布和可能性分布的平均值。由于先验分布较短且分散，所以它反映了人们并不太确定人类的平均身高是多少。同时，可能性在相对较窄的范围内汇总了数据，因此它对真是参数值更加确定。

当先验分布和可能性分布被合并时，数据（由可能性表示）支配了之前那个在巨人堆里长大的人的弱先验信念。尽管那一个体仍然认为人类平均身高比数据告诉他的稍高些，但他最相信的是数据。

3.1 目标

在回顾了上述概念后，我们可以轻易的说明，MCMC算法如何服务于建模用户行为模式。

MCMC算法解决后验概率分布估计问题的思路为：

1. 对于复杂的问题，我们都采用蒙特卡洛法，即采用随机采样的策略，估计样本的后验分布$p(x)$ [2]。
2. 对于复杂的概率分布$p(x)$，我们往往无法直接对其进行采样，此时我们将引入“接受-拒绝采样”，即设定一个容易采样的分布$q(x)$（通常为高斯分布），然后按照一定的方法拒绝某些样本，以达到接近$p(x)$分布的目的 [2]。
3. 对于高维分布，我们一般只能得到条件概率分布，而非联合概率分布，这时我们无法使用“接受-拒绝采样”，另外，对于高维分布，寻找合适的$q(x)$也很困难 [2]。
4. 但如果我们要建模的后验分布是一个随机过程，且该随机过程是马尔可夫链，马尔科夫链模型中状态转移矩阵$\mathbf{P}$的性质可以让我们由任意一个初始分布开始，推断出$n$次状态转移后收敛了的平稳后验分布 [3]。
5. 然而，给定一个平稳的分布，马尔可夫链中的转移矩阵$\mathbf{P}$还是无法得到，因此可以引入MCMC采样，该采样方法使得目标矩阵$\mathbf{P}(i,j)$可以由通过任意一个马尔科夫链状态转移矩阵$\mathbf{Q}$乘以$\alpha(i,j)$得到，即$\mathbf{P}(i,j)=\mathbf{Q}(i,j)\alpha(i,j)$。$\alpha(i,j)$一般称之为接受率。取值在$[0,1]$之间，可以理解为一个概率值 [4]。
6. 后续的，Metropolis-Hastings采样与Gibbs采样都是在MCMC采样的基础上，针对运算复杂度、高维分布拓展性所做出的算法改进。需要指出的是：Gibbs采样在高维特征时有明显优势，因此通常意义上的MCMC采样都是用的Gibbs采样。当然Gibbs采样是从M-H采样的基础上的进化而来的，同时Gibbs采样要求数据至少有两个维度，一维概率分布的采样是没法用Gibbs采样的,这时M-H采样仍然成立 [4][5]。

建模用户行为模式的目标在于预测用户在任意时刻处于某种状态的可能性，若用户的模式可以用马尔可夫链来表示，则用户在时刻$t$的状态$s(t)$将仅与状态转移矩阵$\mathbf{P}$和前一个时刻的状态$s(t-1)$有关。因此，推断状态转移矩阵$\mathbf{P}$，就是建模用户行为的重要基础。回顾上述的MCMC算法脉络，可以看出MCMC采样解决了估计状态转移矩阵$\mathbf{P}$的问题。因此，MCMC算法可以被拆解，用于我们实际的用户行为建模问题上。

【临时笔记】

我们可以从那些方面来构造regime

1. 从用户体验层面：通过识别代表用户体验的KPI所属的regime，我们可以分析用户在哪些时间有较差的网络体验，在分析提供了差体验的小区后，我们也许可以在这些差小区内构造多小区之间的异常链路。
2. 从小区交付能力层面：通过小区的历史性能记录，我们将性能相似的小区归为一个regime
   1. 首先，我们可以在相同regime的小区中做异常检测，避免一些小容量小区上的正常KPI被检测为异常，也避免大容量小区上的异常被漏检。
   2. 这种方法将会过滤掉因为小区设计容量导致的体验差，而更专注于网络问题发现上，即：在同一个regime检测出的异常将更代表网络问题。

3.2 Monte Carlo法

[To be continued]

3.3 Markov Chain & 状态转移矩阵的性质

[To be continued]

3.4 MCMC采样

[To be continued]

4. 案例分析与实现

4.1 开源代码调研

1. statsmodels.tsa（时间序列分析包，github 7k stars）[6]

关键参数说明：

• k_regimes: 设定的regime个数，作为超参数；

2. Python版 regime-switching model（github 9 stars）[7]

关键参数说明：

• n_components: 设定的regime个数，作为超参数；

3. Matlab版 regime-switching model（github 36 stars）

特性说明：

• 支持单维和高维时间序列的建模；
• 可选择模型中的哪些参数随时间切换状态；
• 支持任意数量的regime设置与可解释变量；

本节鸣谢Tongji DNA Lab的Chengbo Qiu同学。

4.2 案例分析

[To be continued]

Reference

[1] https://zhuanlan.zhihu.com/p/32982140

[2] https://www.cnblogs.com/pinard/p/6625739.html

[3] https://www.cnblogs.com/pinard/p/6632399.html

[4] https://www.cnblogs.com/pinard/p/6638955.html

[5] https://www.cnblogs.com/pinard/p/6645766.html

[6] Kim, Chang-Jin, and Charles R. Nelson. 1999. “State-Space Models with Regime Switching: Classical and Gibbs-Sampling Approaches with Applications”. MIT Press Books. The MIT Press.

[7] Ma, Ying, Leonard MacLean, Kuan Xu, and Yonggan Zhao. “A portfolio optimization model with regime-switching risk factors for sector exchange traded funds.” Pac J Optim 7, no. 2 (2011): 281-296.